(5분 읽기)
전자가 실제로 분할할 수 없는 기본 입자임을 확인케 한다.
프랑스 소르본느 물리학자들 초저온 루비듐 원자 사용.
이전에 세슘원자 간섭 측정으로 얻은 값과 일치 하지 않아.
불일치 원인 찾아야 할 과제 남아.

미세 구조 상수의 새로운 값
물리의 기본 크기는 표준 모델을 확인하고 암흑 물질 후보를 줄인다.
 
물리학자들이 미세 구조 상수에 대해 현재까지 가장 정확한 값을 결정했다.
이 상수는 빛과 하전된 입자의 기본적인 상호 작용을 설명하는 상수다. 새로운 값은 이전 측정보다 거의 3배 더 정확하며, 무엇보다도 전자가 실제로 분할할 수 없는 기본 입자임을 확인케 한다. 연구자들이 ’Nature‘에 보고한 것처럼 암흑 물질 입자에 대한 후보 영역을 더욱 좁힌다. 

▲ 좀머펠드(Sommerfeld) 흉상, 뮌헨, LMU, Theresienstr. 37. 흉상 아래에는 미세구조상수의 공식이 있다.

미세 구조 상수는 자연의 기본적인 양 중 하나다.
물리학에서 α로 표기되는 이 상수는 전자기 상호 작용의 강도를 나타낸다.
무엇보다도 빛이 전자 또는 뮤온과 같은 하전된 기본 입자와 얼마나 강하게 상호 작용하는지를 나타낸다.
다른 많은 기본 수량과 양자-물리적 상호 작용이 이 상수에서 파생되기 때문에 물리적 표준 모델의 결정적인 기반이 된다. 따라서 가능한 한 정확하게 아는 것이 중요하다.

레이저 충격을 받은 초저온 루비듐 원자

파리 소르본 대학의 레오 모렐(Leo Morel)과 함께 일하는 연구원들은 현재까지 미세구조 상수에 대한 가장 정확한 값을 결정했다. 그들은 원자가 광자를 흡수하고 일종의 반동을 경험할 때 에너지 상태를 변경한다는 사실을 사용했다. 반동의 속도는 원자의 질량을 알려준다.
알려진 전자의 질량과 수소 원자에서 전자의 결합 에너지를 조합해서 미세구조상수를 계산할 수 있다.

연구진은 초저온 루비듐 원자를 실험에 사용했다. 루비듐 원자는 자기장과 레이저 펄스의 도움으로 진공관에서 들어 올려 측정 구간을 통과하게 된다.
여기에서 원자는 광자를 포착하고 반동으로 여러 측정 레이저의 위상을 미묘하게 바꾼다.
이로부터 Morel과 그의 팀은 반동 속도를 결정한 다음 이를 역수 값 1/α로 미세 구조 상수 계산의 기초로 사용했다.

실제 소립자로 확인된 전자

결과는 미세 구조 상수에 대해 현재까지 가장 정확한 값이다.
따라서 역수 값은 α^-1 = 137.035999206(11)이다. 괄호 안의 숫자는 불확실성 요인을 나타낸다. 연구원에 따르면 이것은 8.1 x 10^-11 또는 810억분의 1이다.
Morel과 그의 팀에 따르면 이것은 이전 측정보다 거의 3배 더 정확하다.
이 값을 사용하면 표준 모델의 다른 상수 및 기본 예측도 확인할 수 있다.

“이 결과는 전자가 하부 구조가 없고 실제 기본 입자임을 확인시켜 준다”고 연구에 참여하지 않은 버클리 캘리포니아 대학의 물리학자 홀거 뮐러(Holger Müller)는 첨부된 주석에서 설명했다. “전자가 더 작은 단위로 구성되어 있다면 자기 모멘트가 다를 것이다.”
후자는 미세 구조 상수에서 파생될 수 있다.

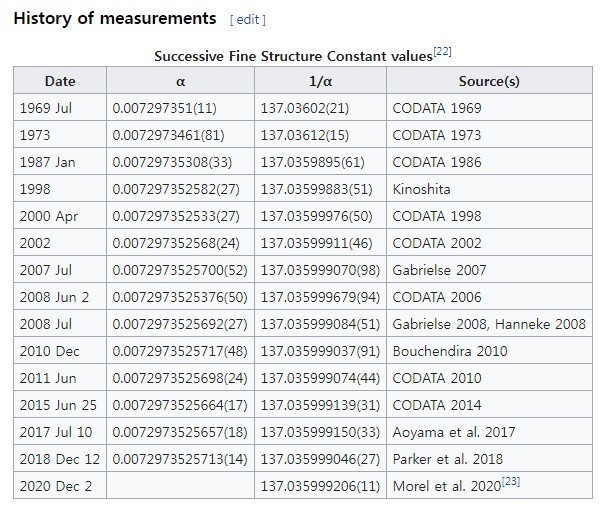▲ 미세구조상수가 결정된 역사

암흑 물질 후보에 대한 통찰력

최근 측정은 우주의 ‘어두운 면(dark side)’에 대해 많은 것을 보여준다.
미세 구조 상수의 더 정확한 값은 암흑 물질 입자가 가질 수 있는 가능한 특성을 더욱 제한하기 때문이다. 여기에는 일부 연구자들이 이테르븀 또는 베릴륨의 양자 점프의 이상 현상을 기반으로 가정한 가상의 힘입자 ‘다크 보손(Dark Boson)’과 같은 후보가 포함된다.

이전 측정값과 결합된 현재 값은 Morel과 그의 팀이 보고한 것처럼 이러한 입자 후보의 존재를 거의 완전히 배제한다. 이 다크-보손은 미묘하지만 측정 가능한 방식으로 전자의 자기 모멘트에 영향을 주어야 하기 때문이다. 그러나 현재 결정된 미세 구조 상수는 이러한 영향을 나타내지 않는다.

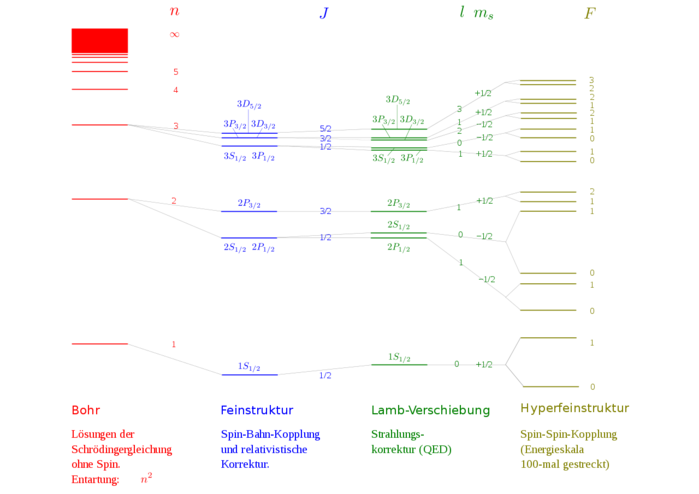▲ 미세 구조 상수는 전자기 상호 작용의 강도, 빛과 전자의 상호 작용도 나타낸다. 수소 원자의 에너지 준위 분할

이전 측정과의 혼란스러운 불일치

그러나 새로운 측정에는 한 가지 의문이 제기된다.
미세구조상수의 새로운 값은 현재까지 가장 정확하지만 이전에 측정된 값과 비교했을 때 표준 편차가 5개 이상 벗어난다. 여기에는 Morel과 그의 동료들이 수행한 측정값과 뮐러와 버클리에 있는 그의 팀이 세슘 원자의 원자 간섭 측정을 통해 결정한 값이 포함된다.

“실험자들은 이제 이러한 불일치의 원인을 명확히 하고 표준 모델을 다시 테스트할 준비를 하고 있다”고 Müller는 말했다.

<참고 : 미세구조상수가 탄생하기까지>
물리학에서 일반적으로 α(그리스 문자 알파)로 표시된다. 좀머펠드 상수(Sommerfeld)상수라고도 불린다. 이 상수는 기본 하전 입자 간의 전자기 상호 작용의 강도를 정량화하는 물리적 기본 상수다. 

 

이것은 4πε0ħcα = e^2의 공식에 의해 기본 하전 입자와 전자기장의 결합 강도를 나타내는 기본 전하 e와 관련된 차원이 없는 양이다. 그 수치는 대략1/137, 사용된 단위 체계와 무관하다.
α에 대한 물리적 해석은 여러 가지가 있지만 1916년에 도입한 Arnold Sommerfeld(독일 물리학자)의 이름에서 원자의 Bohr 모델을 확장할 때 그 이름이 붙여졌다. 

아놀드 좀머펠드(Arnold Sommerfeld)는 Bohr 모델을 확장하여 속도에 대한 질량의 상대론적 의존성과 타원형 궤도를 포함했다. 그가 1916년에 미세 구조 상수라는 용어를 도입했다. 미세 구조 상수 α의 첫 번째 물리적 해석은 상대론적 Bohr 원자의 첫 번째 원형 궤도에서 전자의 속도와 진공에서의 빛의 속도의 비율로 해석되었다. 

이것은 닫힌 궤도에 대해 상대성이 허용하는 최소 각운동량과 양자역학에 의해 허용되는 최소 각운동량 사이의 몫이었다.
이 상수는 1928년 폴 디락(Paul Dirac)의 선형 상대주의 파동 방정식이 정확한 미세 구조 공식을 제공하기 전까지는 중요하지 않은 것으로 여겼다. 

양자전기역학(QED)의 발달로 α의 중요성은 분광 현상에서 전자기장에 대한 일반적인 결합 상수로 확장되어 전자와 광자 간의 상호 작용 강도를 결정한다.
’α/2π‘는 QED의 선구자 중 한 명인 Julian Schwinger의 묘비에 변칙적인 자기 쌍극자 모멘트의 계산을 참조하여 새겨져 있다.
(Nature, 2020; doi : 10.1038 / s41586-020-2964-7)
출처 : Nature, CNRS

[더사이언스플러스=문광주 기자] "No Science, No Future"

[저작권자ⓒ the SCIENCE plus. 무단전재-재배포 금지]